Zero Noise Extrapolation with pyQuil and parametric compilation

In this example we demonstrate how to use Zero Noise Extrapolation (ZNE) in Mitiq with a parametrically compiled program in pyQuil. Parametric compilation saves time by compiling the program ansatz once, instead of compiling each time the parameters are updated. In pyQuil, a memory_map argument is used to substitute in values for previously-declared Quil variables in the pre-compiled executable.

When adding the noise mitigation function zne.execute_with_zne the memory_map is still passed to the executor function and the circuit parameters are updated without the need for repeated compilation.

The example shown here is adapted from the pyQuil parametric compilation tutorial.

import numpy as np
from pyquil import get_qc, Program
from pyquil.gates import RX, RY, H, CNOT, MEASURE
import mitiq
from mitiq import zne
from scipy import optimize

Use the get_qc command to initialize the simulated noisy device where the PyQuil program will run.

# initialize the quantum device
qc = get_qc("2q-noisy-qvm")

Set up the quantum circuit

program = Program()
theta = program.declare("theta", memory_type="REAL")
ro = program.declare("ro", memory_type="BIT", memory_size=1)
program += RX(theta, 0)
program += RY(theta, 0) 
program += RX(theta, 1)
program += RY(theta, 1)
program += H(0)
program += CNOT(1,0)
program += H(0)
program += MEASURE(0, ro[0])

Mitiq’s zne.execute_with_zne function takes a quantum program (e.g. PyQuil program) and an executor function as arguments. The executor function must output the expectation value resulting from running the quantum program.

def expectation(theta, executable: Program) -> float:
    bitstrings = qc.run(
        executable.write_memory(region_name="theta", value=theta)
    ).readout_data.get("ro")
    result = np.mean(bitstrings[:, 0])
    return result

Run the parameter scan without noise mitigation

program.wrap_in_numshots_loop(1000)
quil_prog = qc.compiler.quil_to_native_quil(program, protoquil=True)

thetas = np.linspace(0, 2 * np.pi, 21)
results = []
for theta in thetas:
    results.append(expectation(theta, quil_prog))

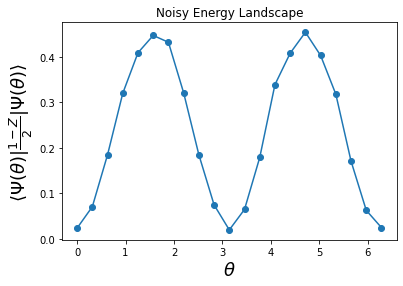
Plot the energy landscape without noise mitigation

from matplotlib import pyplot as plt
_ = plt.figure(1)
_ = plt.plot(thetas, results, 'o-')
_ = plt.xlabel(r'$\theta$', fontsize=18)
_ = plt.ylabel(r'$\langle \Psi(\theta) | \frac{1 - Z}{2} | \Psi(\theta) \rangle$', fontsize=18)    
_ = plt.title('Noisy Energy Landscape')
plt.show()

Run optimization without noise mitigation

quil_prog = qc.compiler.quil_to_native_quil(program, protoquil=True)
init_angle = [0.1]
res = optimize.minimize(expectation, init_angle, args=(quil_prog), method='COBYLA')
print(res)

     fun: 0.021
   maxcv: 0.0
 message: 'Optimization terminated successfully.'
    nfev: 20
  status: 1
 success: True
       x: array([-0.08955312])

Now run parameter scan with ZNE

quil_prog = qc.compiler.quil_to_native_quil(program, protoquil=True)
init_angle = [0.1]
results_zne = []
# here we use a linear fit for the zero noise extrapolation
fac = mitiq.zne.inference.LinearFactory(scale_factors=[1.0, 3.0])
for theta in thetas:
    results_zne.append(
        zne.execute_with_zne(quil_prog, lambda p: expectation(theta, p), factory=fac)
    )

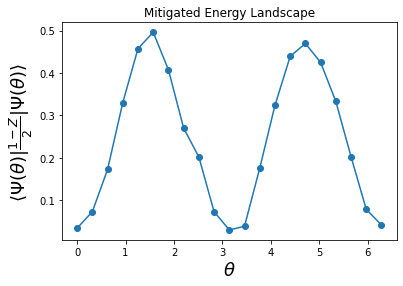
Plot the energy landscape with ZNE

_ = plt.figure(2)
_ = plt.plot(thetas, results_zne, 'o-')
_ = plt.xlabel(r'$\theta$', fontsize=18)
_ = plt.ylabel(r'$\langle \Psi(\theta) | \frac{1 - Z}{2} | \Psi(\theta) \rangle$', fontsize=18)    
_ = plt.title('Mitigated Energy Landscape')
plt.show()

Run optimization with ZNE

def mitigated_expectation(thetas, executable: Program, factory) -> float:
    mitigated_exp =  zne.execute_with_zne(quil_prog, lambda p: expectation(thetas, p), factory=factory)
    return mitigated_exp

quil_prog = qc.compiler.quil_to_native_quil(program, protoquil=True)
res_zne = optimize.minimize(mitigated_expectation, init_angle, args=(quil_prog, fac), method='COBYLA')
print(res_zne)

     fun: 0.016000000000000007
   maxcv: 0.0
 message: 'Optimization terminated successfully.'
    nfev: 20
  status: 1
 success: True
       x: array([-0.04267812])

References

[1] Parametric compilation tutorial in pyQuil.

display information about Mitiq, packages, and Python version/platform

mitiq.about()

Mitiq: A Python toolkit for implementing error mitigation on quantum computers
==============================================================================
Authored by: Mitiq team, 2020 & later (https://github.com/unitaryfund/mitiq)

Mitiq Version:	0.13.0dev

Core Dependencies
-----------------
Cirq Version:	0.13.1
NumPy Version:	1.20.3
SciPy Version:	1.7.3

Optional Dependencies
---------------------
PyQuil Version:	3.0.1
Qiskit Version:	0.32.1
Braket Version:	1.14.0

Python Version:	3.7.7
Platform Info:	Linux (x86_64)